Da es bisher wenig (und zum Teil nicht vollständig aufgeschrieben) zu MAT 29 gibt habe ich meine Notizen so detailliert gemacht wie es mir möglich war
Detailaufgaben:
Aufgabe 1:
Lösen sie folgendes Gleichungssystem:
2*x1 + 0*x2 + 1*x3 - 2*x4 = 3
-2*x1 +0*x2 + 0*x3 + 2*x4 = 2
6*x1 + 0*x2 + 3*x3 + 0*x4 = 3
2*x1 + 1*x2 + 0*x3 - 2*x4 = 1
Hier waren A B C D Gefordert, aber OHNE Rechenschritte, NUR das Ergebnis
-----------------------------------------------------------------------------------------------------
Aufgabe2:
Berechnen sie die Winkel zwischen den Vektoren ab ac bc
a: (-1,0,2,0)
b: (3,-1,5,2)
c: (0,1,1,2)
Hier waren nur die Winkel gefordert, auch hier kein Rechenweg.
->siehe Formel arcos ( skalarprodukt(ab) / ( betrag(a) * betrag (b) ) )
-----------------------------------------------------------------------------------------------------
Aufgabe 3:
Berechnen sie a2-a5 der GEOMETRISCHEN Folge
a1 = 32
a6=3152
Auch hier NUR Ergebnis, kein Rechenweg
-----------------------------------------------------------------------------------------------------
Aufgabe 4:
Gegeben ist die Folge :
500,200,80,32
Frage -> Handelt es sich um eine geometrische oder eine Arithmetische Folge ?
Frage -> Konvergiert oder Divergiert diese Folge
Frage -> Nennen sie den Grenzwert der REIHE bis auf 2 Stellen nach dem Komma gerundet
Auch hier, nur Antworten, kein Rechenweg
Aufgabe 5
Gegeben sind:
Ebene -> E: x - 2y -3z = 4
Gerade -> g : (x,y,z) = (0,-5.4) + 1 * (1,2,3)
(Die Klammern sollen bei der Geraden in Vektorenschreibweise sein)
Frage -> Berechnen sie den Schnittpunkt der Geraden mit der Ebene
Auch hier, nur Ergebnis kein Rechenweg
-----------------------------------------------------------------------------------------------------
Komplexaufgaben:
Folgen und Reihen:
Habe ich leider nicht beantwortet und auch keine Zeit mehr zum Lesen gehabt :-/
-----------------------------------------------------------------------------------------------------
Geraden und Ebenen
Es sind 4 Punkte gegeben
P1 (0,0,0)
P2 (1,1,2)
P3 (0,2,-1)
P4 (1,1,1)
Frage -> Bestimmen sie die Ebene der Punkte P1, P2 und P3
Frage -> Bestimmen sie den Normalenvektor der Ebene und stellen sie die Ebene in Normalform
Frage -> Berechnen sie die Schnittpunkte der Ebene mit den Achsen des Koordinatensystems
Frage -> Berechnen sie den Abstand von Punkt P4 zur Ebene
-----------------------------------------------------------------------------------------------------
Matrix Rechnung
Hier war eine Firma gegeben welche Produkte 1-4 herstellt
Diese Produkte hatten verschiedene Kosten
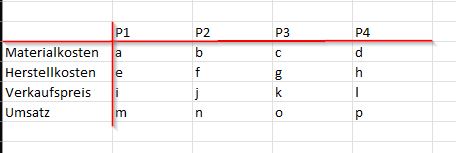
(Die Buchstaben die ich eingesetzt habe waren gegebene Zahlen in der Einheit GE für Geldeinheiten)
Vorgegeben war diese Aufgabe in einem Freitextfeld welches mit einer Tabelle als Darstellungsform für die erweiterte Matrix genutzt wird.
Es gab Anforderungen was der Betrieb erreichen will:
Materialkosten nicht höher als 42
Herstellkosten nicht höher als 70
Verauspreis von 34
Umsatz von 292
Frage -> Wieviele Einheiten kann der Betrieb von P1,P2,P3,P4 herstellen ?
Frage -> Welchen Rang hat die Matrix
Frage -> ist das Gleichungssystem lösbar ? Begründen sie ihre Antwort
TIPP: Schaut euch hierzu bitte in WM111 die Aufgabe 4 und 18 von S36 an, sie liegen seeehr nahe bei einander.
-----------------------------------------------------------------------------------------------------
Ich danke allen die ihre Erfahrungen zu MAT29 geteillt haben, besonders den Beiträgen von Tobi169 und Naive113
Ps Schaut euch auch noch die Zusammenfassungen von MAT22 an, da hier einiges sehr ähnlich ist.
Im Anhang findet ihr eine PDF mit den Wichtigsten Formeln zu Ebenen und Geraden, die Screenshots habe ich von STUDIFLIX entnommen.
Ich empfehle euch da wirklich die ganzen Videos zu Normalenvektor Normalenform,Schnittpunkt Ebene und Gerade, Parameterform in Ebenenform, Abstandsformel,Parameterform in Koordinatenform zu suchten.
PS PS: Holt euch den Casio FX-991DEX für die Klausur und übt früh genug damit, der ist hier GOLD wert.


